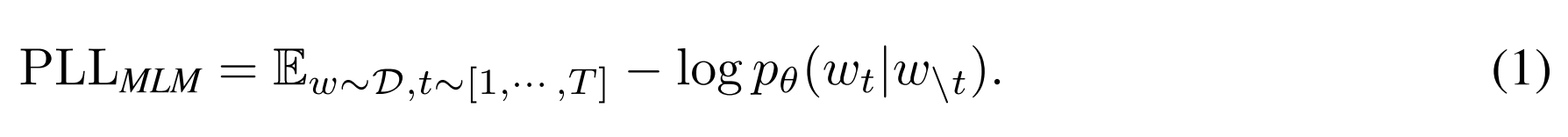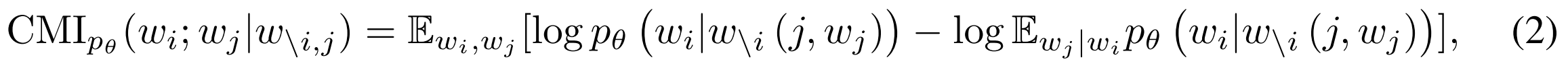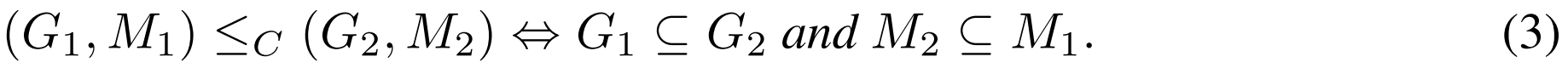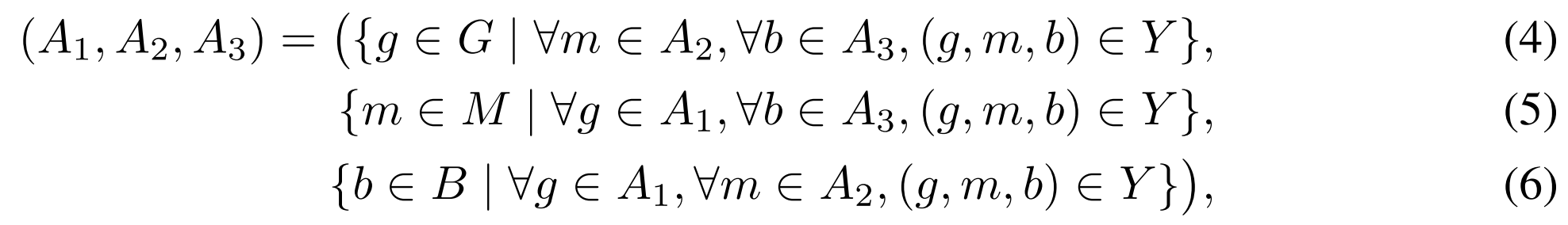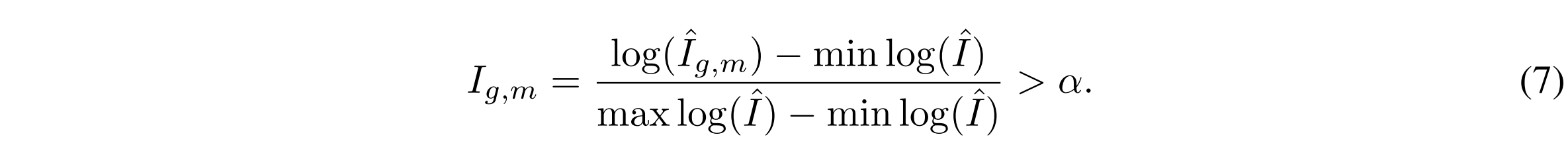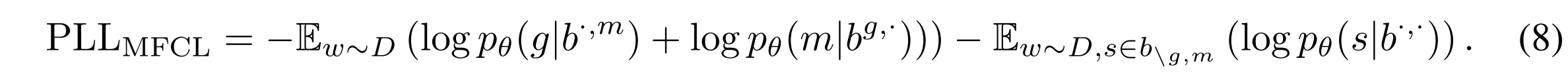From Tokens to Lattices: Emergent Lattice Structures in Language Models

Xiong, Bo, and Steffen Staab. “From tokens to lattices: emergent lattice structures in language models.” (2025).

What problem does this paper address?

Conceptualization of masked language models (MLMs), i.e.
the ability to capture conceptual knowledge, and understanding concepts as well as their hierarchical relationships.

What is the motivation?

Pitfalls of existing work:

focus exclusively on concepts included in human-defined ontology,
overlook “latent” concepts that extend beyond human definitions,
do not explain how conceptualization emerges from MLM pretraining.

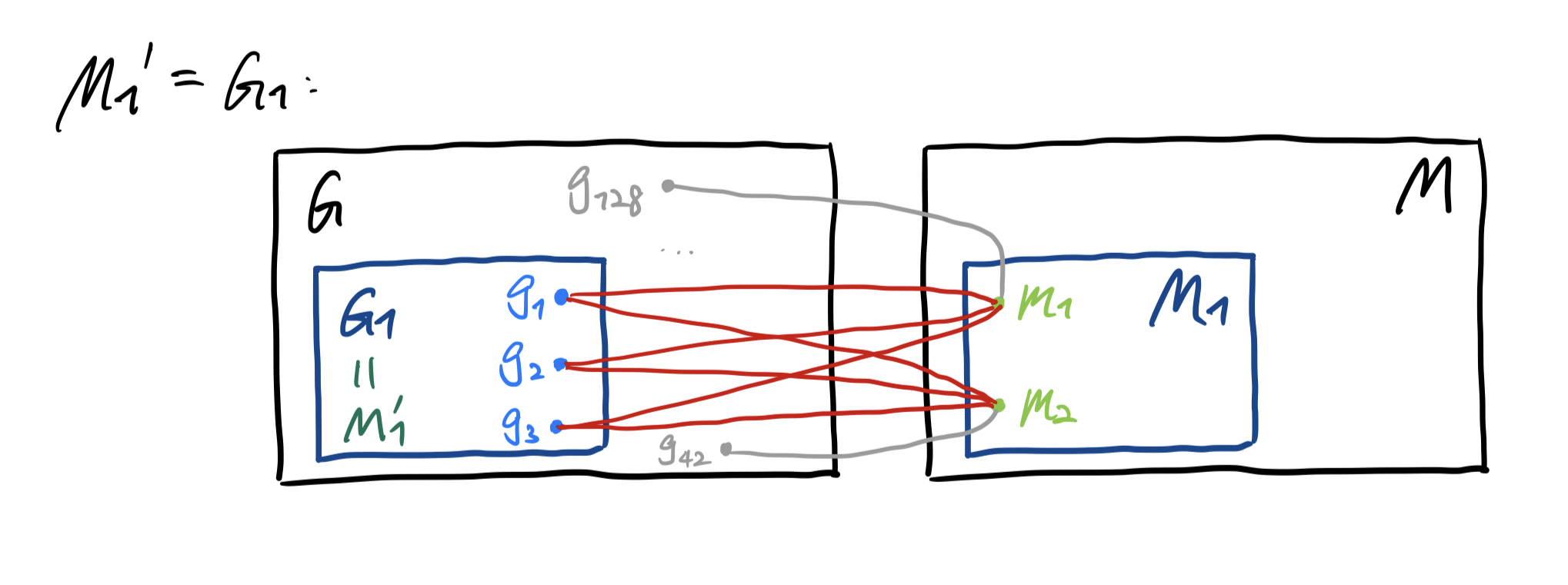
How is MLM defined in this paper?

: an input sequence of tokens, each taking a value from a vocabulary
= : the masked sequence after replacing the -th token with a special token
A masked language model (MLM) predicts using its bidirectional context .
: the data generating distribution
MLM learns a probabilistic model that minimizes the pseudo log-likelihood loss
MLMs can be interpreted as the non-linear version of Gaussian graphical models, where
- token random variables that form a fully-connected undirected graph
- Assumption: Each random variable is dependent on all the other random variables, and learn the dependencies across tokens.
- The cross-token dependencies can be identified by conditional mutual information (CMI), i.e. the pointwise mutual information (PMI) conditioned on the rest of the tokens:
where denotes the sentence substituting with a new token .

How is the term “concept” defined in this paper?

A “concept” is defined as: the abstraction of a collection of objects that share some common attributes.

What is Formal Concept Analysis (FCA)?

FCA is a mathematical theory of lattices for reconstructing a concept lattice from the observations of objects and their attributes.
These observations of objects and attributes are represented by a formal context, defined as a triple , where
- : a finite set of objects
- : a finite set of attributes
- : a binary relation (“incidence”) between objects and attributes, with each element indicating whether an object possesses a particular attribute .
- can be represented by the following matrix:
A formal concept is a pair defined as follows:
- ,
- set of all attriubtes shared by the objects in (是中的所有对象共同拥有的属性的集合)
- set of all objects sharing the attributes in (是共同拥有中所有属性的对象的集合)
- is a formal concept iff the set of all attributes shared by the objects in is identical to , and dually, the set of all objects that share the attributes in is identical to , i.e. and .
  - is called the extent of
  - is called the intent of
  Explanation of the conditions:
  is an object subset (“target object set”), is an attribute subset (“target attribute set”).
  - : The shared attributes of all objects in are exactly the target attributes.
  - : The objects sharing all attributes in are exactly the target objects.
The inclusion of between objects/attributes induces a partial order relation of formal concepts, defined by
- top concept , bottom concept
- For any formal concept :
FCA can be extended to deal with 3D data where the object-attribute relations depend on certain patterns by introducing the triadic formal context, defined as a quadruple where
- : a finite set of objects
- : a finite set of attributes
- : a finite set of conditions (i.e. patterns)
- : a ternary relation between object possessing attribute under condition .
A triadic concept of the triadic formal context is a triple where
, , , and
- : the set of objects sharing all attributes in under all conditions in
  (在中所有条件下共同拥有中所有属性的对象的集合)
- : the set of attributes shared by all objects in under all conditions in
  (在中所有条件下被中所有对象共同拥有的属性的集合)
- : the set of conditions under which all objects in share all attributes in
  (一组条件的集合，在这些条件下，中所有对象共享中所有的属性)

What is Concept Lattice?

Concept lattice is an abstract structure comprising the set of all concepts and the partial order relation given in a formal context. It describes the inclusion relationship between the sets of objects and attributes.

How does the definition of “concept” relate to the mathematical foundation of FCA?

By characterizing concepts as sets of objects and attributes, the partial order relations (偏序关系) between concepts are naturally induced from the inclusion relations (包含关系) of the corresponding sets of objects and attributes, which are indepedent from human-defined structures.

What are the differences between Definitional Hypothesis and Distributional Hypothesis?

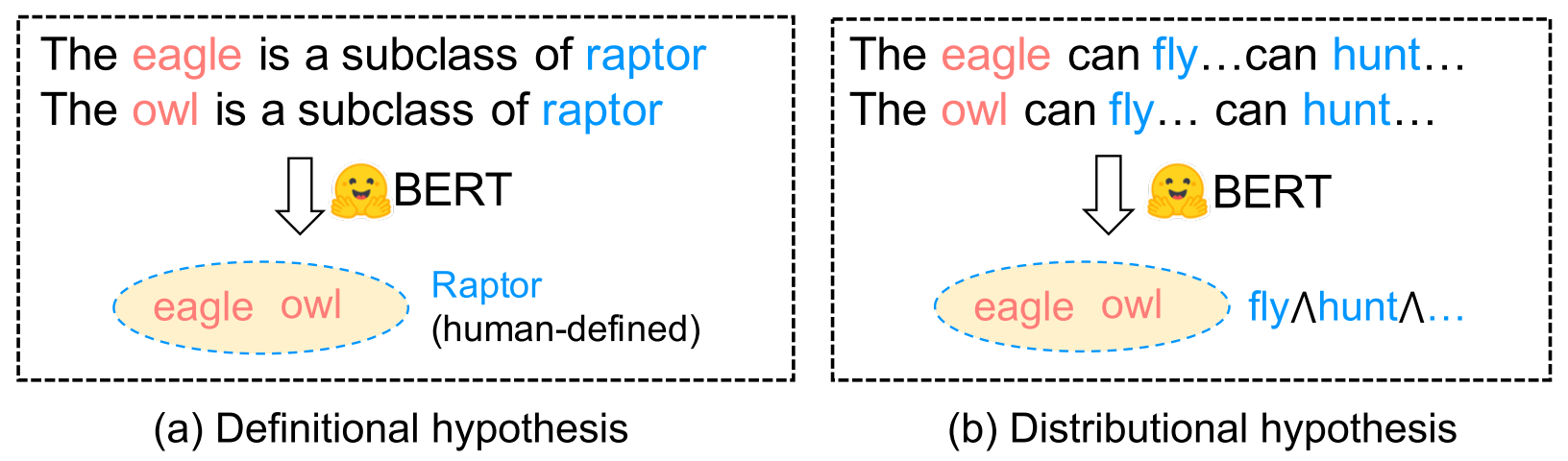
Definitional Hypothesis: Concepts are explicitly defined in the text and directly learned from these definitions.

Limitations:
- Such grounding or conceptualization is typically not frequently found in non-wikipedia and non-handbook texts or conversations.
- It relies on human-defined concept names as the “definition” and cannot handle “latent” concepts whose names are not explicitly defined by human.
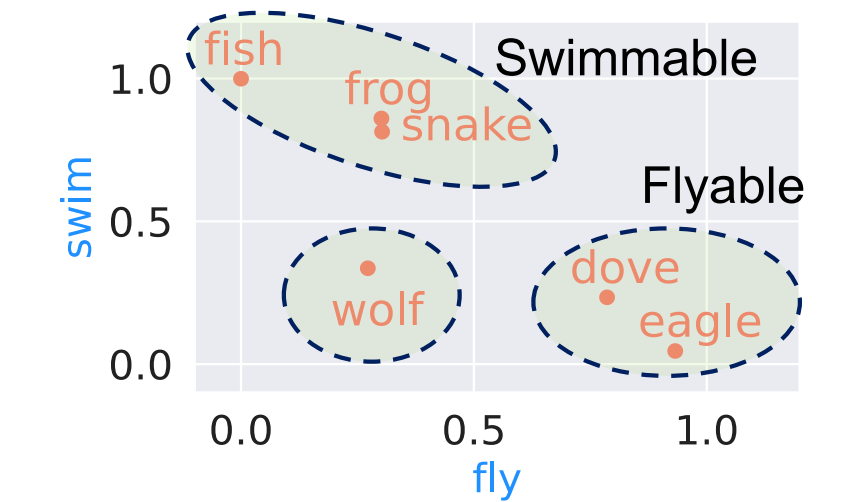
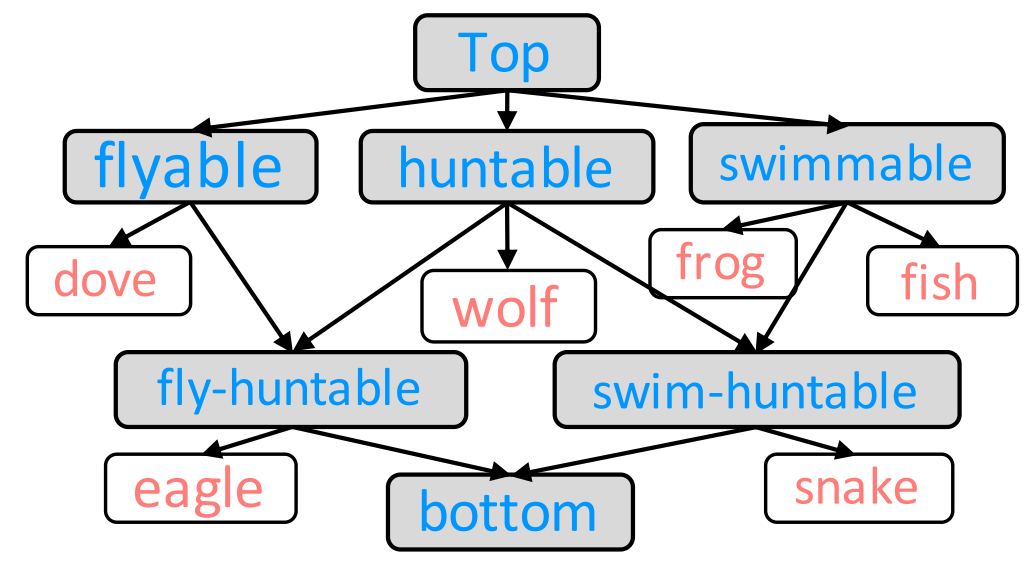
- Example: There is no popularly used term specifying birds that can swim and hunt, but they are indeed a formal concept in the context of FCA.

Distributional Hypothesis: Similar concepts have similar attributes. Concepts are learned from the observations of their attributes.

Example: The human-defined concept raptor is a rarely used term in texts, while the attributes fly and hunt are more frequently used in texts.

What are the research questions?

RQ1: How does the conceptualization emerge from MLM pretraining?
RQ2: How are concept lattices constructed from MLMs?
RQ3: What is the origin of the inductive biases of MLMs in lattice structure learning?
RQ4: Can conditional probability in MLMs recover formal context?
RQ5: Can the reconstructed formal contexts correctly identify concepts?

What is the main hypothesis?

Based on the distributional hypothesis, the conceptualization of MLMs emerges from the learned dependencies between the latent variables representing the objects and attributes. MLMs implicitly model concepts by learning a formal context through conditional probability distributions between objects and attributes in a target domain.

What are the main contributions?

This paper shows that MLMs are implicitly performing FCA, i.e. they implicitly model objects and attributes as masked tokens, and model the formal context by the conditional probability between objects and attributes under certain patterns. As a result, a concept lattice can be approximately recovered from the conditional probability distributions of tokens given some patterns through FCA.
This paper proposes a novel and efficient formal context construction method from pretrained MLMs using probing and FCA.
This paper investigates the origin of the inductive biases of MLMs in lattice structure leanring.
This paper creates 3 evaluation datasets, and provides theoretical analyses and empirical results verifying the main hypothesis.

RQ1: How do MLMs learn conceptual / ontological knowledge from natural language?

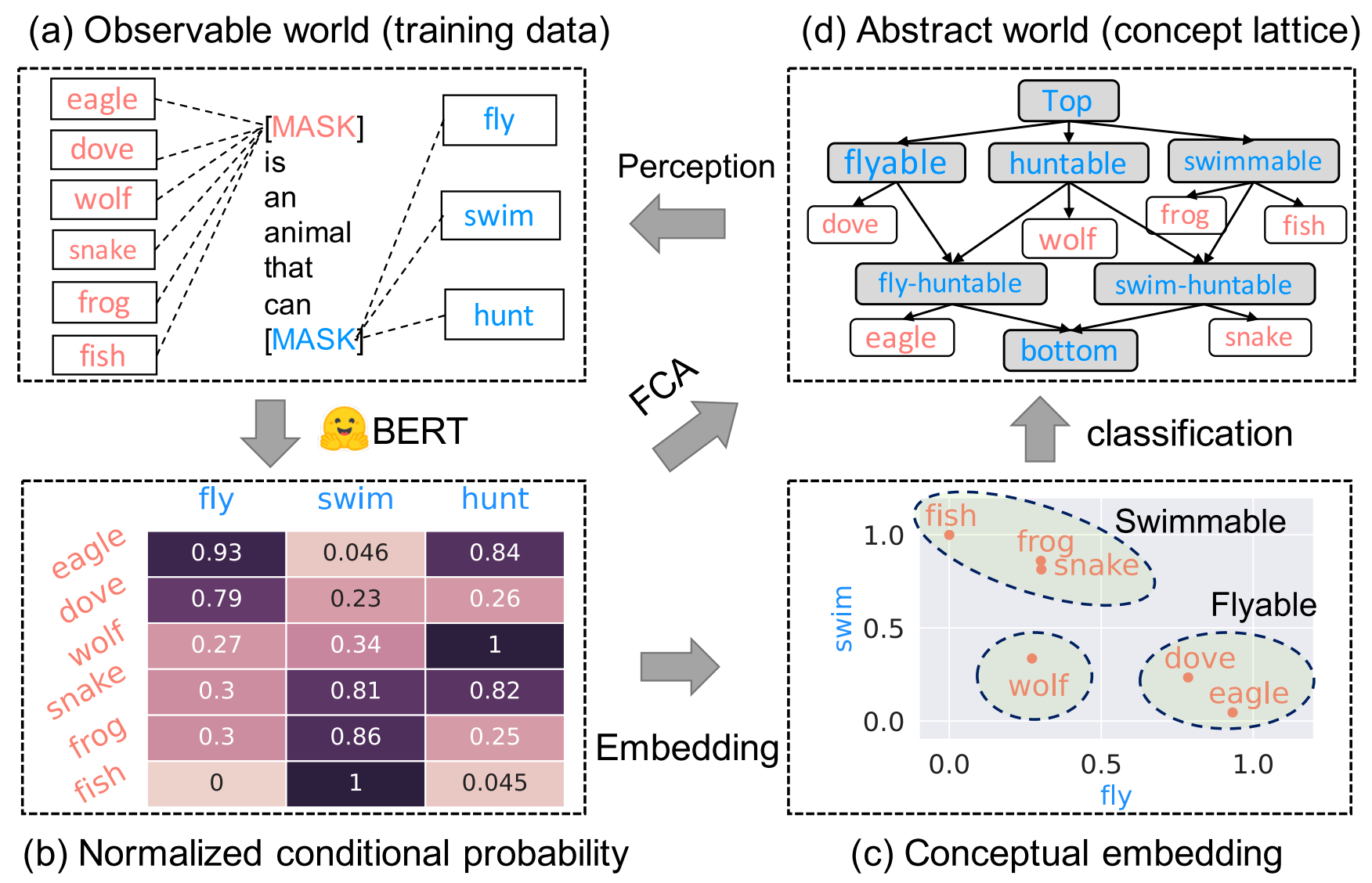
(a). Observable World (Training Data)

The observation is a set of sentences describing relationships between objects and attributes.
Each sentence is abstracted as a filling of a pattern with an object-attribute pair.
- Example:
  Pattern (template):
  Filling of a pattern forms a sentence:

(b). Normalized Conditional Probability

The normalized conditional probability between objects and attributes is learned by the MLM, and can be viewed as a formal context in a probabilistic space.

(c). Conceptual Embedding

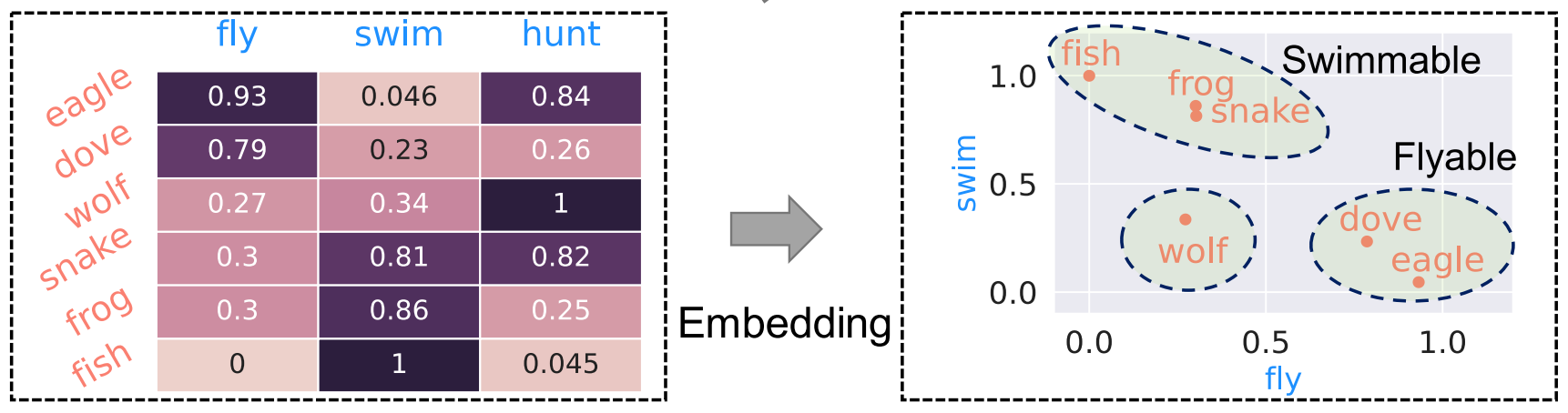
Each row of the conditional probability matrix represents the conceptual embedding of a particular object.
Each column of the conditional probability matrix represents the conceptual embedding of a particular attribute.
These dimensionally interpretable embeddings can be used for concept classification.

(d). Abstract World (Concept Lattice)

The concept lattice can be recovered from the learned formal context in (b) through FCA, and can be viewed as a hierarchy for concept classification.

RQ2: How are concept lattices constructed from MLMs using FCA?

The relationship between objects and attributes can be explored by probing using a cloze prompt.
pattern (): template with object and attribute tokens being masked
filling of (): the instantiation of a pattern with a specific object-attribute pair
partial fillings of pattern :
- : filling with object alone
- : filling with attribute alone

Probabilistic triadic formal context

Estimate conditional dependencies between objects and attributes using and .

Construct a conditional probability matrix serving as an approximation of the formal context. This is achieved by cataloging all possible fillings of objects and attributes within a concept domain.

Challenge: The accuracy of this formal context largely depends on the pattern’s (i.e. template’s) efficacy in capturing the intended concept domain and its ability to mitigate confounding influences from other factors.

Solution:

Utilize multiple patterns (templates).
Construct a probabilistic triadic formal context (represented as a 3D tensor).

Construction of probabilistic triadic formal context:
Input:

a pretrained MLM
a set of objects and a set of attributes the model has been trained on
a set of patterns

Output: triadic formal context

, or
where , ,

Challenge: Constructing the complete three-way tensor involves a complexity of .

Solution: a new efficient method for constructing probabilistic triadic formal context

Assumption:

Considering the top most informative patterns is sufficient for the construction.
This renders the time complexity nearly linear: or evaluations of cloze prompt
- : batch size
- : ceiling function

Method:
Let denote the predicted conditional probability vector given , and given a set of objects , a set of attributes , and a pattern , we construct (resp. ) such that its -th row (resp. ) denote the partial filling of pattern with attribute (resp. object ).

Let (resp. ) be the token indexes of objects (resp. attributes ), the formal context of pattern can be reconstructed by

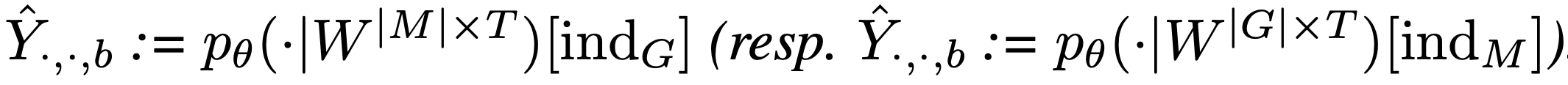
Core idea of the above method:

Extract the conditional probability over all possible tokens in a batch-wise manner, and then
index the relevant conditional probabilities using the object indices or attribute indices.

Limitation: Either objects or attributes must be included in the MLM’s vocabulary. Construction relies on pre-defined sets of objects and attributes within a domain.

Alternative: Generate set of object-attribute pairs in the domain from the distribution.

Challenge: Direct sampling from the joint distribution via Markov Chain Monte Carlo (MCMC) sampling is challenging.

Insight towards a solution: MLMs can function as probabilistic generative models.
Solution: formal context generation via Gibbs Sampling

Input: an MLM + a concept pattern
Sample an initial object directly from and then an attribute from .
At each subsequent step , sample a new object from and then a new attribute from .
This results in a sequence of object-attribute pairs: .
Compute the conditional probabilities for all objects and attributes based on this sequence.
Output: reconstructed probabilistic triadic formal context .

Lattice construction:

smoothed version of discrete triadic formal context conceptual embedding
Approximate probabilistic incidence matrix by aggregating over multiple patterns, through either
- mean pooling: , or
- max pooling:
Binarization using min-max normalization:
Generate all formal concepts by identifying combinations of objects and attributes that fulfill the closure property in the aforementioned definition of formal concept.
Structure these formal concepts into a lattice based on the partial order relation.

RQ3: What is the origin of the inductive biases of MLMs in lattice structure learning?

Conclusion:

The inductive bias of MLMs in lattice structure learning originates from the learned conditional dependency between tokens. The precision of the lattice construction depends mainly on the quality of the chosen pattern in exclusively capturing the object-attribute relationship.

Details:

Natural language concept analysis: Conceptualization arises from observing the attributes present in objects.

Formalize a word model as a ground-truth formal context .

Formalize a data point as a sentence describing that an object has a particular attribute, obtained by filling a concept pattern with an object-attribute pair sampled from .

Data generation process:

Input: a ground-truth formal context (world model) , a set of concept patterns
Sample a concept pattern i.i.d. from (i.i.d.: independently and identically distributed).
Sample an object-attribute pair i.i.d. from .
Generate a data point by filling with .
Output: a data point , where , , , and .

Goal of formal context learning: Reconstruct the world model (i.e. the original formal context) from the data points generated by the above data generation process.

Challenge: Real-world data generation processes are not ideal and might be influenced by other factors or noises. An exact reconstruction of the original formal context is hence improbable.

Solution: -approximate formal context learning
Given a set of data points generated by the above data generation process, derive a probabilistic formal context incidence matrix from , s.t. the distance .

Hypothesis: Identify the formal context incidence matrix from the generated sentences is possible.

Masked Formal Context Learning (MFCL):

Insight: MLM objective non-linear version of Gaussian graphical models Lasso regression
MFCL objective: minimize the pseudo log-likelihood loss
- first two terms: encourage capturing object-attribute dependencies under certain pattern (, )
- third term: the quality of the chosen pattern significantly influences the effectiveness of formal context learning
  Insight: A pattern might contain irrelevant or confounding information (characterized as latent variable information ) that confuses the learning of object-attribute dependency.

Role of the choice of pattern:

: CMI without latent variables
: CMI with latent variables
The difference between the CMIs without and with latent variables is bounded by the conditional entropy :
If the concept pattern provides sufficient information that uniquely describes the object-attribute relationship without introducing confounding factors (i.e. ), then the CMI directly captures the object-attribute dependency.
The quality of the chosen pattern is crucial for accurately capturing the object-attribute relations.

Summarization of the method:

Design templates (concept patterns).
Predict the conditional probabilities between objects and attributes ( or ) using an MLM.
Reconstruct the smoothed version of the discrete probabilistic triadic formal context using the predicted conditional probabilities via Gibbs sampling.
Construct the concept lattice from the reconstructed smoothed formal context:
- Approximate the probabilistic incidence matrix by mean-pooling or max-pooling multiple patterns.
- Convert to a binary-valued matrix using min-max normalization.
- Generate all formal concepts from the observations of object-attribute pairs.
- Apply FCA to structure these formal concepts into a concept lattice based on the partial order relations given in the formal context.

Formal Context Datasets

Three new datasets of formal contexts in different domains (serving as gold-standards for evaluation):

Region-language:
- official languages used in different administrative regions around the world
- extracted from Wiki44k
- relatively sparser
Animal-behavior:
- most popular single-token English animal names, with 25 behaviors based on animal attributes
- human-curated
- relatively denser
Disease-symptom:
- single-token diease names and their symptoms
- extracted from the Kaggle Disease Symptom Description dataset
- relatively sparser

Three concept patterns for each dataset:

RQ4: Can conditional probability in MLMs recover formal context?

Experiment

Compare the formal contexts reconstructed from the conditional probabilities with gold-standards.
Ranking problem
Evaluation metrics:
- Mean Reciprocal Rank [1, 2, 3]:
- Hit Rate [3]:
Models: BERT-base-uncased, BERT-distill-uncased, BERT-large-uncased, BioBERT
Baseline: BertEmb

Result

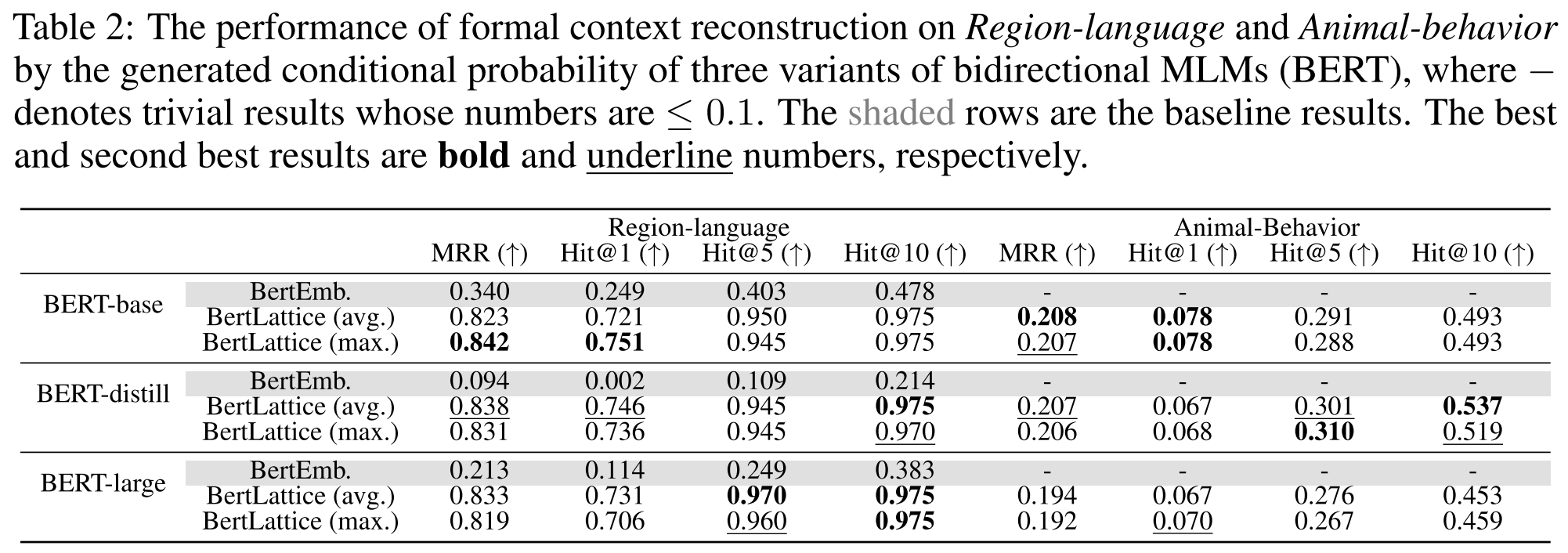
All variants of > on Region-language and Animal-behavior.
Within Disease-symptom, results on popular diseases > unpopular ones.

Conclusion

The conditional probabilities in MLMs can recover formal contexts.
Observation frequency significantly influences MLM’s ability to learn correct object-attribute relationships.

RQ5: Can the reconstructed formal contexts identify concepts correctly?

Experiment

Classify objects by determining whether they possess all the attributes of a given concept, using the conditional probability under the given patterns.
Multi-label concept classification problem
Evaluation metrics:
- F1 score
- mean Average Precision (mAP)

Result

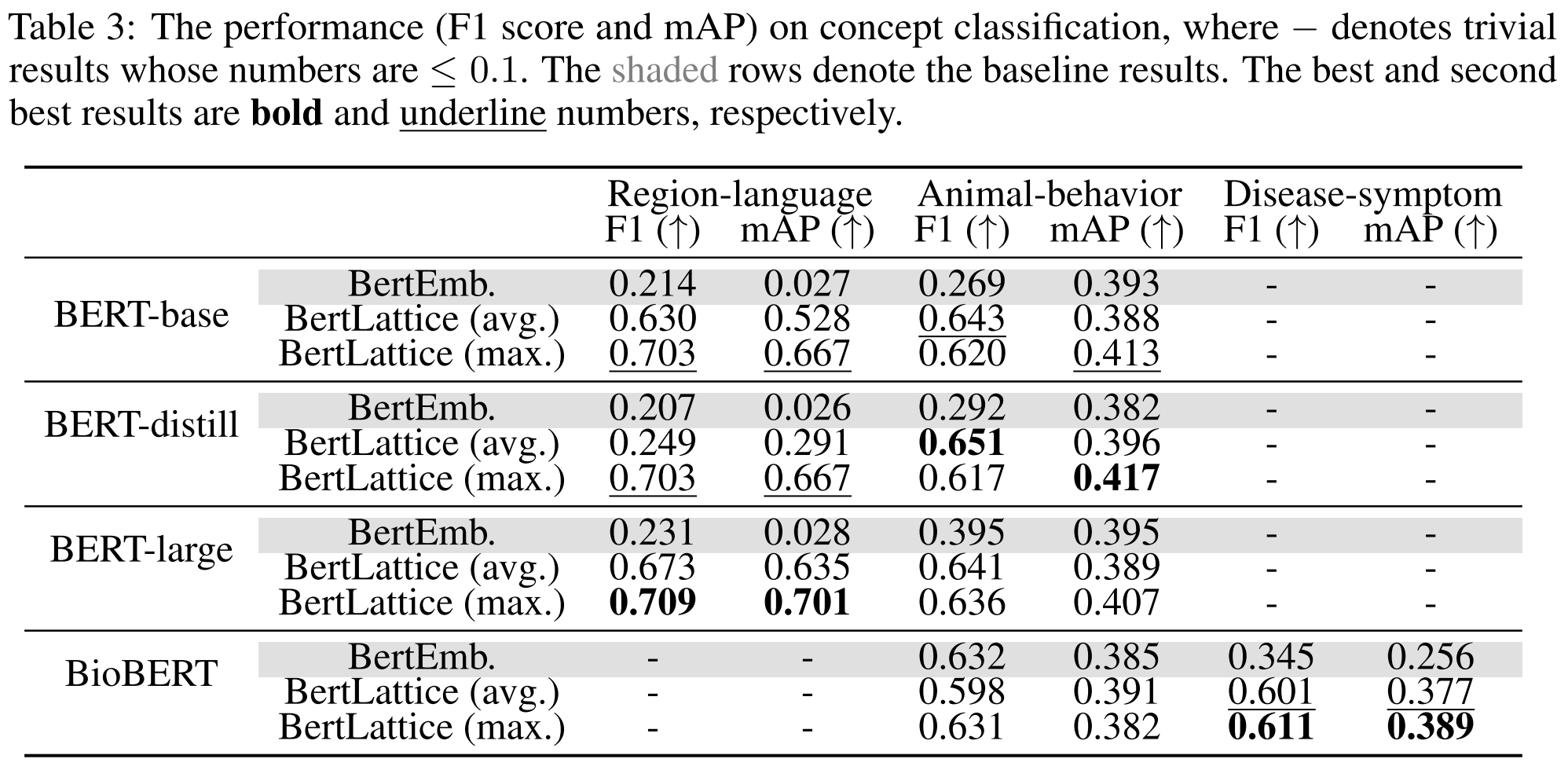
All variants of > on all three datasets.

Conclusion

The constructed formal contexts can efficiently identify concepts.
The model discovers some latent concepts that have not been pre-defined by humans, e.g.,
“” and “”.

Answers to the RQs

RQ1: How does the conceptualization emerge from MLM pretraining?

The conceptualization of MLMs emerges from the learned dependencies between the latent variables representing the objects and attributes.

RQ2: How are concept lattices constructed from MLMs?

After binarization, a concept lattice is contructed by
- generating all formal concepts by identifying combinations of objects and attributes, and
- structuring these formal concepts into a concept lattice.

RQ3: What is the origin of the inductive biases of MLMs in lattice structure learning?

The inductive bias of MLMs in lattice strcture learning originates from the learned conditional dependencies (i.e. conditional probabilities) between the tokens.

RQ4: Can conditional probability in MLMs recover formal context?

The formal contexts reconstructed through conditional probabilities are indeed more effective than the embedding method.
The conditional probabilities can better reconstruct those object-attribute relations that occur more frequently in the training data.
MLMs can indeed reconstruct the formal context of Disease-Symptom through the conditional probabilities.

RQ5: Can the reconstructed formal contexts correctly identify concepts?

All variants of BertLattice outperform BertEmb on all three datasets. Yes.

What are the strengths and weaknesses of this paper?

Strengths

This paper establishes a new connection between MLMs and FCA based on rigorous experiments and analysis.
The proposed method is highly innovative in theory and has clear logic.
The proposed method can discover latent concepts that are not pre-defined by human.
The proposed method does not rely on pre-defined concepts or ontologies.
The proposed method does not require training or fine-tuning the model.

Weaknesses

The datasets contain limited number of concept patterns, which are not representative considering the diverse patterns existing in diverse real-world data sources.
The authors did not explain why direct sampling from the joint distribution via MCMC is challenging.
The authors did not systematically investigate how to design effective concept patterns that can exclusively capture the object-attribute relationship.
The method may not be trivially adaptable to autoregressive LMs (e.g., GPT series).
The method is limited to single-relational data.

What insights does this paper provide?

The Masked Language Modeling (MLM) training objective implicitly learns the conditional dependencies between the latent variables representing objects, attributes and their relationships under certain patterns (templates), which can be interpreted as a probabilistic formal context.
The learned probabilistic formal context enables the reconstruction of the underlying concept lattices through FCA.
The inductive bias of MLMs in lattice structure learning originates from the learned conditional probabilities between tokens.
The quality of the chosen pattern is crucial for accurately capturing the object-attribute relations and hence the precision of the lattice construction.
The formal contexts reconstructed through conditional probabilities between objects and attributes are more effective than the last-hidden layer embeddings of objects and attributes.
The conditional probabilities can better reconstruct those object-attribute relations that occur more frequently in the training data.
Min-max normalization is more robust than sigmoid normalization for concept lattice reconstruction.
The reconstructed concept lattice contains “latent concepts” that are not explicitly defined by human.