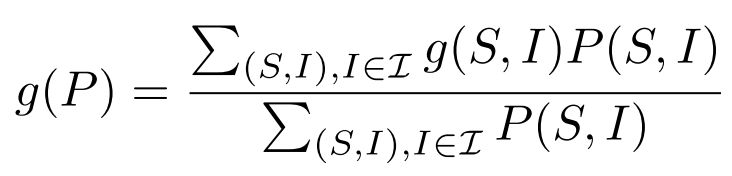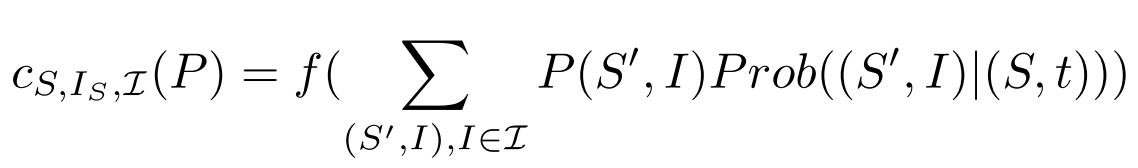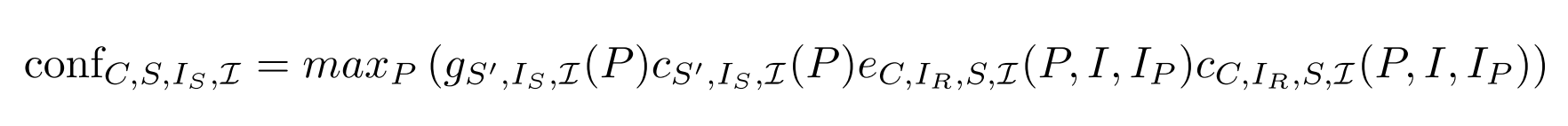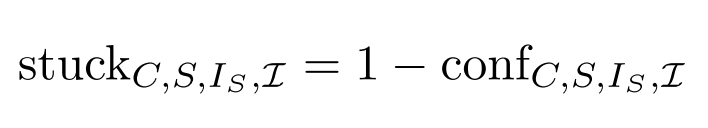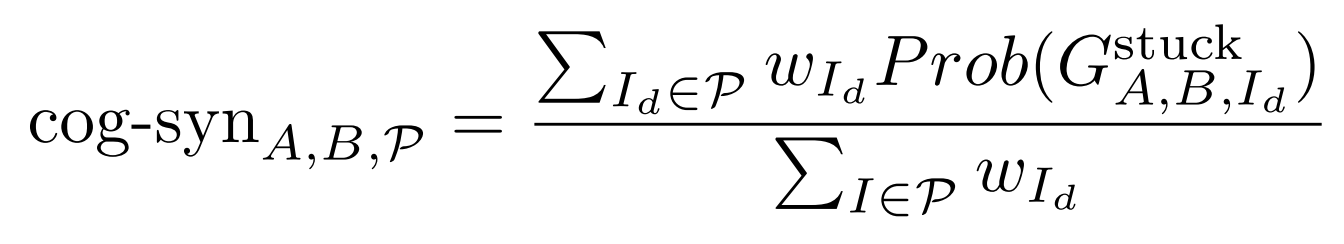Toward a Formal Model of Cognitive Synergy

Ben Goertzel. (2017). Toward a formal model of cognitive synergy. arXiv preprint arXiv:1703.04361.

What problems does this paper address?

The formalization of cognitive synergy in the language of category theory, and its relationship with Artifical General Intelligence (AGI).
The evaluation of the degree of cognitive synergy ebabled by existing or future concrete AGI designs.

What’s the motivation of this paper?

Humanlike minds form only a small percentage of the space of all possible generally intelligent systems.
–> Research Question: Do there exist general principles which any system must obey in order to achieve advanced general intelligence using feasible computational resources?
The current mathematical theory of general intelligence focuses mainly on the properties of general intelligences that use massive, infeasible amounts of computational resources.
Current practical AGI work focuses on specific classes of systems that are hoped to display powerful general intelligence.
The level of the generality of the underlying design principles is rarely clarified.

What are the main contributions of this paper?

This paper revisits the concept of cognitive synergy and gives a more formal description of cognitive synergy in the language of category theory.
This paper proposes a hierarchy of formal models of intelligent agents.
This paper evaluates the degree of cognitive synergy enabled by existing or future concrete AGI designs.
This paper formally describes the relationships between cognitive synergy and homomorphisms, and that between cognitive synergy and natural transformation.
This paper introduces some core synergies of cognitive systems, such as consciousness, selves and others.

What is cognitive synergy?

Basic concept of cognitive synergy: General intelligence must contain different knowledge creation mechanisms corresponding to different sorts of memory, such as declarative, procedural, sensory / episodic, attentional, and intentional memory. These mechanisms must be interconnected in such a way as to aid each other in overcoming memory-type-specific combinatorial explosions.
Conceptual definition: A dynamic in which multiple cognitive processes, which coorperate to control the same cognitive system, assist each other in overcoming bottlenecks encountered during their internal processing.
Within Probabilistic Growth and Mining of Combinations (PGMC) agents, based on developing a formal notion of “stuckness”, cognitive synergy is defined as a relationship between cognitive processes in which they can help each other out when they get stuck.

Hierarchy of the formal models of intelligent agents:

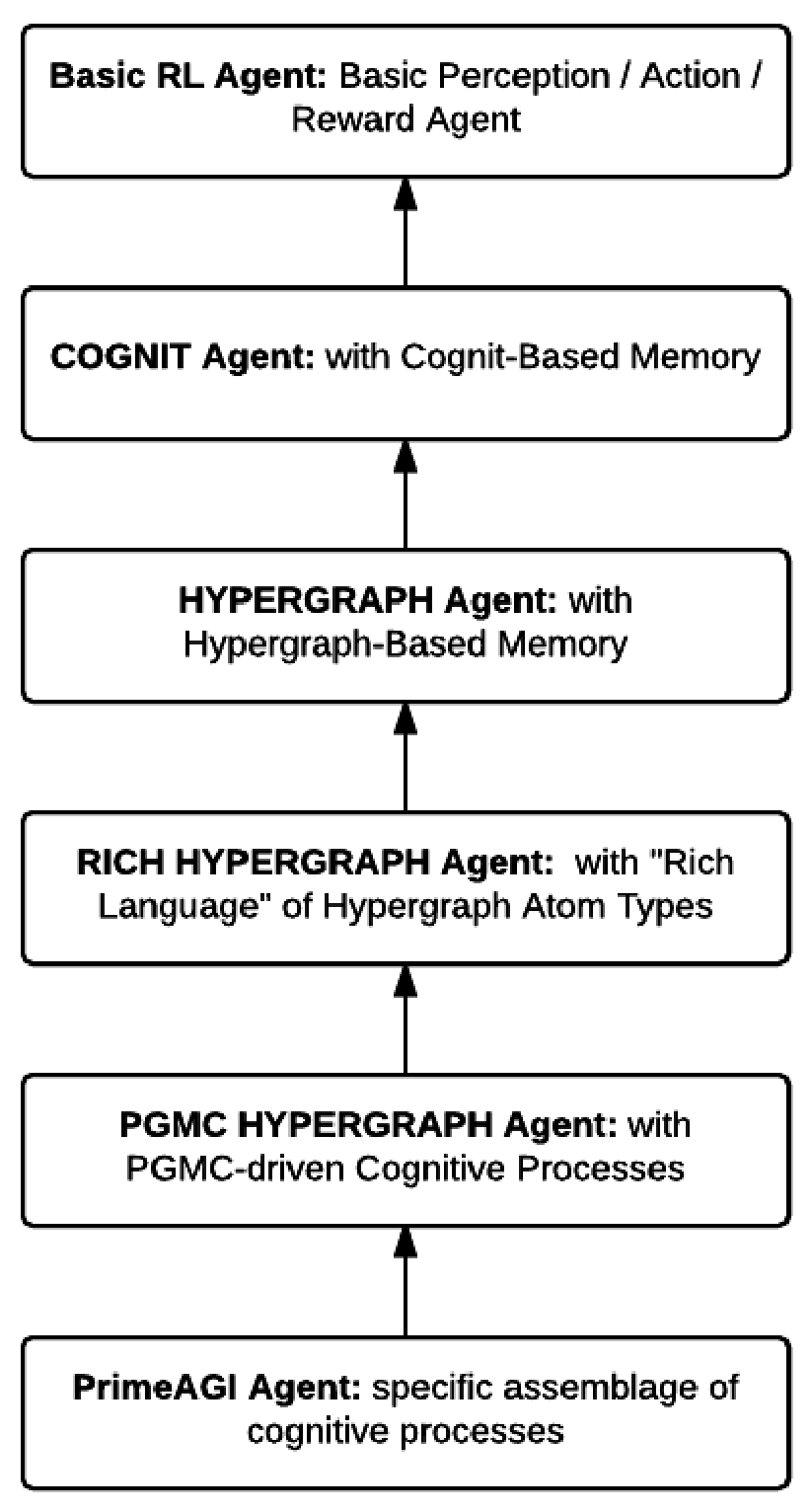
(Most generic at the top, most specific at the bottom.)

Basic Reinforcement Learning (RL) Agents

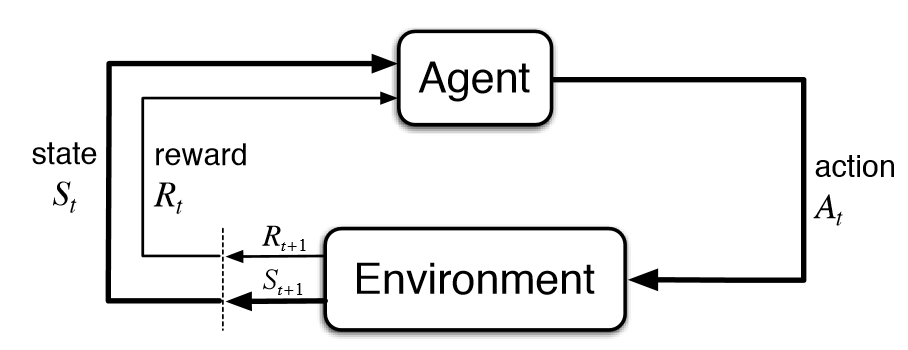
A class of active agents which observe and explore their environment, take actions that may change the state of the environment, and update their behaviors to maximize the expected cumulative rewards received from the environment in the long run.
Markov Decision Process (MDP): a classical formalization of sequential decision making, where actions affect not only immediate rewards, but also subsequent states and future rewards.
Markov property: The probability of each possible value for the state and reward depends only on the immediately preceding state and action.

Agent sends symbols from a finite action space to the environment, i.e. taking an action.
The environment sends signals to the agent with symbols from a state space
Agent receives a reward from the reward space .

The agent and environment are understood to take turns sending signals back and forth, yielding a history (“trajectory”) of states, actions and rewards: s₀, a₀, r₁, s₁, a₁, r₂, … , s_i, a_i, r_i+1, …
The agent is represented by a policy function which maps a state to probabilities of selecting each possible action .
The dynamic of the environment can be characterized by a probability distribution .
Goal-seeking agent: an agent that receives a goal besides the perception of environment’s states and rewards.

Cognit Agents: agents with cognit-based memory

Introduce a finite set of atomic cognitive actions (aka. atomic cognitions, or “cognits”), denoted as c_i.
Add to the trajectory such that it has the form s₀, c₀, a₀, r₁, s₁, c₁, a₁, r₂, … , s_i, c_i, a_i, r_i+1, …
All these perceptions of states, actions, rewards, goals and cognits are stored in the memory of the agent.
At each time step, the agent carries out internal cognitive actions on their memories and external actions in the environment.
When a cognit is activated, it acts on all the other elements in the memory (despite many NULL results in most cases).
The result of the action of cognition c_i on the element x in the memory may be any of the following:
- causing x to get removed from the memory (“forget”)
- causing some new cognit c_j to get created and persist in the memory (“create”)
- if x is an action, causing x to get actually executed (“execute”)
- if x is a cognit, causing x to get activated (“activate”)
The process of a cognitive action c_i on the memory may take time, during which other perceptions of states and actions may occur.
This cognitive model may be conceived in algebraic terms: Consider as a product in a certain algebra.
Question: Should one allow multiple copies of the same cognit to exist in the memory?
(When a new cognit is created, what if it is already in the memory?)
- If we increase the count of this cognit in the memory, then the memory will become a multiset, and the product of cognit interactions will become a hypercomplex algebra over the non-negative integers.
This setting models the interaction between cognits, and in this way models the actual decision-making, action-choosing actions inside the formal agent.

Hypergraph Agents

Definition: Agents with labeled hypergraph-based memory.
A hypergraph is a graph in which links may optionally connect more than two different nodes.
Assumption: The memory of cognit agents has a more specific structure, i.e. a labeled hypergraph. The nodes and links in the hypergraph may optionally be labeled with strings, or structures of the form (string, vector of numerical values).
- String label indicates the type of the node / link.
- Numerical values in the vector may have different semantics based on the type.
Nodes and links in the hypergraph are collectively denoted as “Atoms”.
The cognits become either Atoms, or sets of Atoms (i.e. subhypergraphs of the overall memory hypergraph).
When a cognit is activated, one or more of the following happens:
1. The cognit produces some new cognit. Optionally, this new cognit may be activated.
2. The cognit activates one or more of the other cognits that it directly links to (or is directly linked to).
  - one important example: The cognit re-activates the cognit that activated it in the first place.
    execution of “program graphs”
3. The cognit is interpreted as a pattern, which is then matched against the entire hypergraph. The matched cognits returned from memory are then inserted into the memory.
4. Other cognits are removed from the memory.
5. Nothing happens.

Rich Hypergraph Agents

Definition: Agents with a memory hypergraph and a rich language of hypergraph’s Atom types.
Assumption: Atom can be assigned labels from {“variable”, “lambda”, “implication”, “after”, “and”, “or”, “not”}
h-pattern: a hypergraph with some of its Atoms labeled with “variable”.
To conveviently represent cognitive processes inside the hypergraph, extend the label space with labels “create Atom”, “remove Atom”.
To take into account the state of the hypergraph at each time point, extend the label space with labels “time”, “atTime”.
The resulting label space is:
{“variable”, “lambda”, “implication”, “after”, “and”, “or”, “not”, “create Atom”, “remove Atom”, “time”, “atTime”}.

CPT graph

The implications representing transitions between two states may be additionally linked to Atoms indicating the proximal cause of the transition.
Assume there are two cognitive processes called Reasoning and Blending. Then these two processes each corresponds to a subgraph containing the links indicating the state transitions, and the nodes connected by these links.
This subgraph is called Cognitive Process Transition Hypergraph (CPT graph).

PGMC Agents

Definition: Agents with a rich hypergraph memory, and homomorphism or history-mining based cognitive processes.
Goal of this formalization: To model the internals of cognitive processes in a more fine-grained and yet still abtract way.

Cognitive Processes and Homomorphism

Hypothesis: The cognitive processes for human-like cognition may be summarized as sets of hypergraph rewrite rules.
A hypergraph rewrite rule has an input h-pattern and an output h-pattern, along with optional auxilliary functions that determine the numerical weights associated with the Atoms in the output h-pattern, which is based on the combination of the numerical weights in the input h-pattern.
Rules of this nature may be (but are not required to be) homomorphisms.
Conjecture 1. Most operations undertaken by cognitive processes take the form:
- merging two nodes into a new node, which inherits its parents’ links (homomorphisms), or
- splitting a node into two nodes, so that the children’s links taken together compose the parent’s links (inverse homomorphisms).
In other words: Most cognitive processes useful for human-like cognition are implemented in terms of rules that are mostly homomorphisms or inverse homomorphisms.

Operations on Cognitive Process Transition Hypergraphs

One can place a natural Heyting algebra structure on the space of hypergraphs, using
- the disjoint union for ,
- the categorical product for , and
- a special partial order called the cost order.
This Heyting algebra structure allows one to assign probabilities to hypergraphs within a larger set of hypergraphs.

What do these Heyting algebra operators mean in the context of CPT graphs?

Suppose two CPT graphs A and B, representing the state transitions corresponding to two different cognitive processes.
A B is a graph representing transitions between conjuncted states of the system.
A B is a graph representing the two state transition graphs.
A^B is a graph whose nodes are functions mapping states of B to states of A.
Definition of cost order: A < A₁ , if (1) A and A₁ are homomorphic, and (2) the shortest path to creating A₁ from irreducible source graph, is to first create A.
In the context of CPT graphs, this will hold if A₁ is a broader category of cognitive actions than A .
For example, if A denotes all facial expression actions, and A₁ denotes all physical actions, then A < A₁ .

PGMC: Cognitive Control with Pattern and Probability

What is Probabilistic Growth and Mining of Combinations (PGMC)?

Hypothesis: There exists a common control logic that spans multiple cognitive processes, i.e. adaptive control based on historically observed patterns.
Consider the subgraph of a particular CPT graph in the system at a specific time point. The Cognitive Control Process (CCP) aims to figure out what a cognitive process should do next to extend the current CPT graph.
What is the answer to this question?
- There are various heuristics. This paper focuses on pattern mining from the system’s history.
Assumptions:
- The system has certain goals, which manifest themselves as a vector of fuzzy distributions over the states of the system.
- a label “goal”
- At any given time, the system has n specific goals.
- For each goal, each state may be assoicated with a number indicating the degree to which it fulfills that goal, i.e. goal-achievement score.
- There is a fixed set of goals associated with the system.
This way, the CCP aims to figure out how to use the corresponding cognitive process to transition the system to states that will possess the highest goal-achievement score.
In this case, the CCP may look at h-patterns in the subset of system history stored in the system, do probabilistic calculations to estimate the odds that a given action on the cognitive process’s part, and yield a state manifesting a given amount of progress on goal achievement.
If a cognitive process selects actions in a stochastic way, one can use the h-patterns inferred from the remembered parts of the system’s history to inform a probability distribution over potential actions.
Selecting cognitive actions based on the distribution implied by these h-patterns can be viewed a novel form of probabilistic programming, driven by fitness-based sampling rather than Monte-Carlo sampling or optimization queries. This is called Probabilistic Growth and Mining of Combinations (PGMC).
Based on the inference from h-patterns mined from history, a CCP can then
- create probabilistically weighted links from Atoms representing h-patterns in the system’s current state, to Atoms representing h-patterns in potential future states
- and optionally, create probabilistically weighted links from Atoms representing h-patterns in present- / potential future states, to goals.

Theory of Stuckness

Motivation: In a real-world cognitive system, each Cognitive Control Process (CCP) will have a limited amount of resources, which it can either use for its own activity, or transfer to another cognitive process.
A CCP is stuck, if it does not see any high-confidence, high-probability transitions, associated with its own corresponding cognitive process, that have significantly higher goal-achievement scores.
If a CCP is stuck, then it may not be worthwhile for the CCP to spend it limited resources on taking any action at that time. In some cases, it may be the best move to transfer some of its allocated resources to other cognitive processes (“cognitive synergy”).

A Formal Definition of Stuckness

Let be the CPT graph corresponding to cognitive process .
is a subgraph of the overall transition graph of the cognitive process in the system.
Given a particular situation (“possible world”) involving the system’s cognition, and a time interval . Let denote the CPT graph of the cognitive process during time interval .
Let be an h-pattern in the system. Let denotes the degree to which the system displays h-pattern in situation during time interval . Let denote the average degree of goal-achievement of the system in situation during .
If we identify a set of time intervals of interest, we can then calculate the degree to which the h-pattern implies goal-achievement in general:
Suppose the system is currently in situation , during time interval . Then might be defined as a set of time intervals in the near future after . Then we can calculate the degree to which implies goal-achievement in situations that may occur in the near future after being in situation :
The confidence of this degree of goal-achievement is:
- where is a monotone increasing function with range [0, 1].
- This confidence measures the amount of evidence on which the estimate is based.
Finally, we may define as the probability estimate that the CCP corresponding to cognitive process C holds for the following proposition:
In situation S during time interval , if allocated a resource amount in interval for making the choice, C will make a choice leading to a situation in which during the interval after . A confidence score may be defined similarly to .
Given a set of time intervals, one can define and via averaging over the intervals in .
The confidence of knowing how to move forward toward the system’s goals in situation at time is then:
The stuckness of a CCP is defined as the complementary value of the confidence of a cognitive process knowing how to move forward towards the system’s goal in a particular situation at a specific time:

Cognitive Synergy

Premise of the existence of cognitive synergy between two cognitive processes and :
For many situations and times , exactly one of and is stuck.
In the metasystem, the set of pairs where exactly one of and is stuck to a degree of stuckness has a certain probability .
The set of CPT graphs and corresponding to the pairs in has a certain probability .
An overall index of cognitive synergy between cognitive processes and is defined as:

where is a partition of [0, 1].

Extension of this definition to more than two cognitive processes:

Given N cognitive processes, consider triplewise synergies between them.
Let , , be three cognitive processes. Then, is defined as the set of where all but one of , , is stuck to a degree in .
The triplewise synergy corresponds to cases where the system get stuck if it had only two of the three cognitive processes.

Cognitive Synergy and Homomorphisms

Conjecture 2: In a PGMC agent operating with feasible resource constraints, if there is a high degree of cognitive synergy between two cognitive processes and , then there will be a lot of low-cost homomorphisms between subgraphs of and , but not nearly so many low-cost isomorphisms.

Intuition:

If the two CPT graphs are too close to isomorphic, then they are unlikely to offer many advantages to each other. They tend to succeed and fail in the same situations.
If the two CPT graphs don’t have some resemblance to each other, then if one of the two cognitive processes (say ) get stuck, the other one (say ) won’t be able to use the information produced by before it got stuck, and won’t be able to proceed efficiently.
Productive synergy happens when one has two processes, each of which can transform the other one’s intermediate results into its own internal language at low cost, where the internal languages of the two processes are different from each other.

Cognitive Synergy and Natural Transformations

: a cognitive process
: a functor that maps to a subset , such that it maps to as well
: a sequence of cognitive operations and conclusions
: the closest match to in which all cognitive operations involved are done by
The cost of may be much higher than the cost of .

A natural transformation from to associates to every object in a morphism in , so that for every morphism in , it holds .

Conjecture 3: In a PGMC agent operating with feasible resource constraints, suppose there are two cognitive processes and , which display significant cognitive synergy, then:
- there is likely to be a natural transformation between functors and , and a natural transformation going in the opposite direction
- often it requires significantly less total cost to
  - travel from to via and and then to via , than to travel from to directly via .

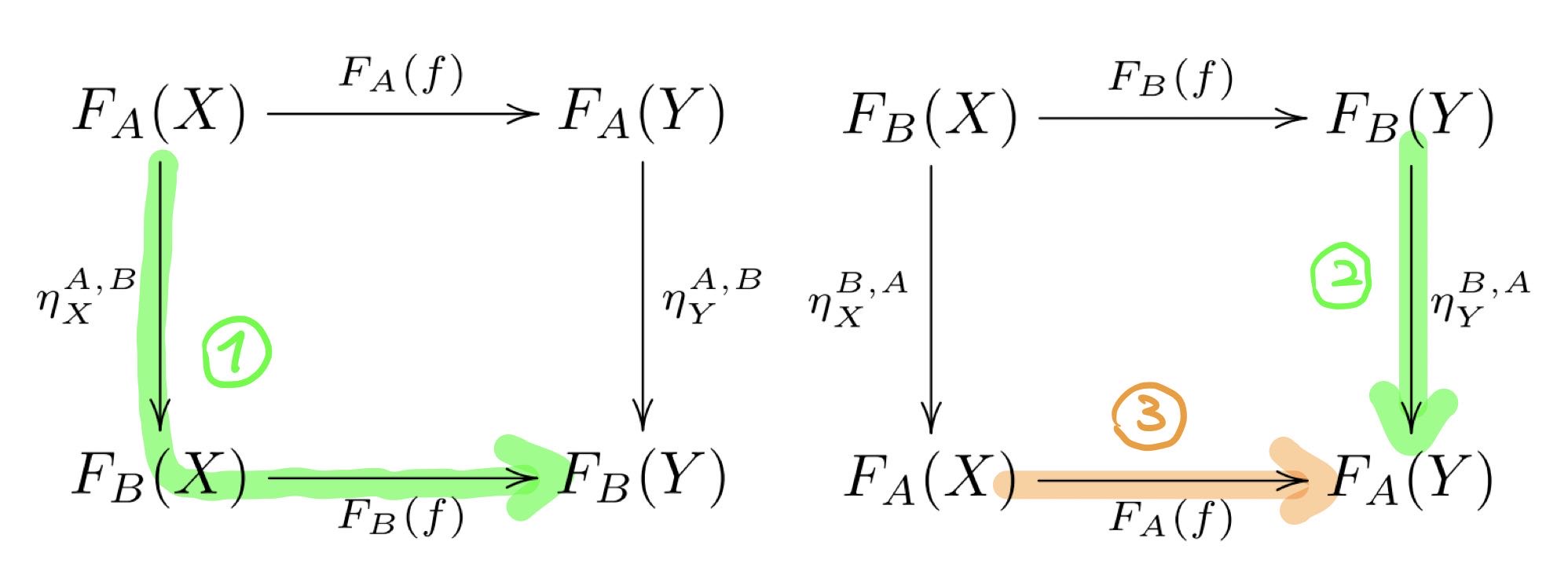
It may sometimes be significantly more efficient to get from to via an indirect route involving cognitive process , than to go directly from to using only the cognitive process .

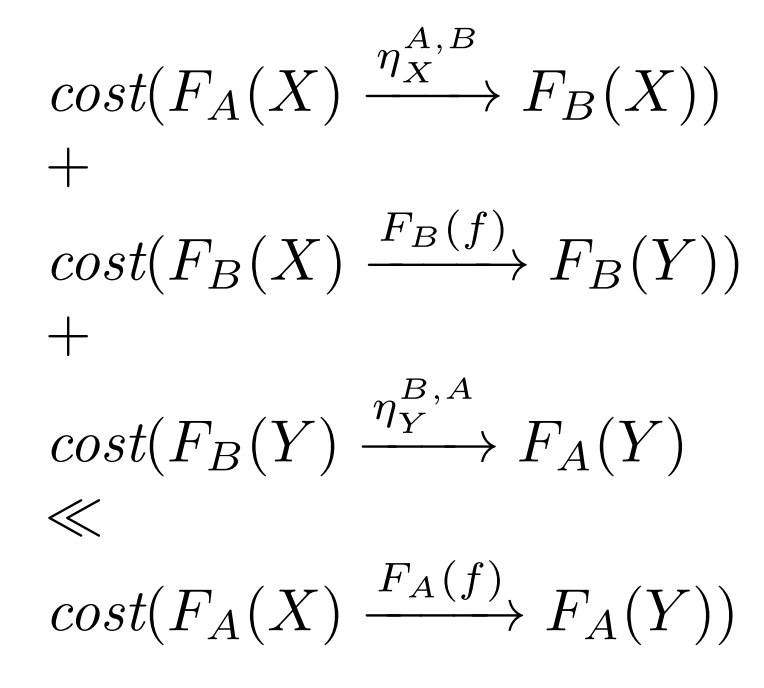
How does Conjecture 1 fits with Conjecture 2?

If we consider and as their own categories, the homomorphisms posited in Conjecture 3 would take the form of functors between these two categories.

Some Core Synergies of Cognitive Systems

It is important to consider cases where two cognitive processes and correspond to different scales of processing, or different types of subsystem of the same cognitive system:
- = long-term memory (LTM), = working memory (WM)
- = whole-system structures and dynamics, = the system’s self-model
- and are different “sub-selves” of the same cognitive system
- is the system’s self-model, and is the system’s model of another cognitive system (e.g., another person, another robot etc.)
Hypotheses:
- Homomorphisms between LTM and WM ensure the ideas can be moved back and forth from one sort of memory to another, with a loss of detail but not a total loss of essential structure.
- Homomorphisms between the whole system’s structures and dynamics and the structures and dynamics in its self-model make the self-model structurally reflective of the whole system.
- Homomorphisms between the whole system in the view of one subself and the whole system in the view of another subself enable the two different subselves to operate somewhat harmoniously together, controlling the same overall system and utilizing the knowledge gained by one another.
- Homomorphisms between the system’s self-model and its model of another cognitive system enable both theory-of-mind type modeling of others, and learning about oneself by analogy to others, which is critical for early childhood learning.

Cognitive synergy in the form of natural transformations between LTM and WM means:
- When an unconscious LTM cognitive process get stuck, it can push relevant knowledge to WM where the solution would pop up.
- When WM gets stuck, it can throw the problem to the unconscious LTM process and hope the answer could be found there and pushed to WM again.
- WM “consciousness”

Hypothesis:
- When we pull a memory into attention, or push something out of attention into the “unconscious”, we are enacting homomorphisms on the state transition graph of our mind.
- The action of the natural transformation between unconscious and conscious cognitive processes:
  - The focus of attention pushes a problem into the unconscious. The unconsious solves the problem and pushes it back into the attentional focus. Then, the answer gets deliberatively reasoned further.
    (顿悟的心理过程：人将问题”交给”无意识处理，之后答案会浮现，并通过有意识的深思熟虑被进一步精细化推理。)
  - This is the case where the cost of going the long way around the commutation diagram from conscious to unconscious and back, is lower than the cost of going directly from conscious premise to conscious conclusion.

Cognitive synergy in the form of natural transformations between system and self means:
- When the system as a whole cannot figure out the solution to a problem, it will map this problem into the self-model and see if cognitive processes acting therein can solve the problem.
- If thinking in terms of the self-model doesn’t figure out a solution to a problem, sometimes “just doing it” is the right approach. This means mapping the problem, which the cognitive processes of the self-model are trying to solve, back to the whole system and see if the whole system can solve it.
Cognitive synergy in the form of natural transformations between subselves means:
- When one subself gets stuck, it may map the problem into the cognitive vernacular of another subself and see if the latter can solve it.
- i.e. switching back and forth between subselves that are well adapted to different sorts of situations.
- This can simulate complex social situations.
Cognitive synergy in the form of natural transformations between self-model and other-model means:
- When one get stuck in a self-decision, one can implicitly ask “What would I do if I were this other mind?”, or “What would this other mind do in this situation?”.
- When one cannot figure out what another mind is going to do via other routes, one can map the other mind’s situation back into one’s self-mind, and ask “What would I do in their situation?”, or “What would it be like to be that other mind in this situation?”.

This sort of “request for help” is most feasible, if
- the problem can be mapped into the cognitive world of the helper in a way that preserves its essential structure, even if not all its details, and
- the answer the helper finds can be mapped back in a similar structure-preserving way.
A key aspect of effective cognition is the ability for the subsystems within a cognitive system to ask each other for help in very granular ways, so that the helper can understand the intermediate state of partial-solution the requestor has found itself in.

Cognitive Synergy in the PrimeAGI Design

Key learning and reasoning algorithms:
- PLN: a forward and backward chaining based probabilistic logic engine, based on the Probabilistic Logic Networks formalism
- MOSES: an evolutionary program learning framework, incorporating rule-based program normalization, prob- abilistic modeling and other advanced features
- ECAN: nonlinear-dynamics-based ”economic attention allocation”, based on spreading of ShortTermImpor- tance and LongTermImportance values and Hebbian learning
- Pattern Mining: information-theory based greedy hypergraph pattern mining
- Clustering and Concept Blending: heuristics for forming new ConceptNodes from existing ones
Curry-Howard correspondence
Some places where the potential for cognitive syerngy exists:
- Pattern mining
- PLN inference
- MOSES